Wie entstand Oversampling?
In Prospekten der Hersteller aus den 80-er Jahren liest man häufig, dass Oversampling aus technischen Gründen notwendig war und zudem die Klangqualität steigere.
Aber wie entstand es wirklich?
Es war Zufall. Ohne den hätte die Geschichte des CD-Standards theoretisch ganz anders ausgehen können.
Schon sehr früh hatte die britische BBC-Rundfunkanstalt eine Digital-Analog-Wandlung mit 13 Bit propagiert.
Philips entwickelte bereits in den 70-er Jahren eine digitale Bildschallplatte, die aber erfolglos blieb.
Die Geräte waren viel zu teuer, nur 400 Stück wurden verkauft, die Niederländer stellten die Produktion rasch wieder ein.
Aber immerhin - das Know how aus diesem Bildplattenspieler floss bei Philips in einen Digital-Analogwandler mit 14 Bit für Audiozwecke ein.
Dann kam Sony als Partner für die CD-Einführung ins Spiel.
Die Japaner empfahlen einen 16-Bit-Standard.
Nach einigem Hin und Her einigten sich Philips und Sony schließlich auf den Digital-Standard von 16 Bit und 44,1kHz.

Aber Philips hatte gar keinen fertigen 16-Bit-Wandler.
Was tun? Die Markteinführung der CD-Technik verzögern?
Niemand kennt die Hintergründe solcher Geschichten besser als die Leute, die damals beteiligt waren.
Kees A. Schouhamer Immink war Mitentwickler dieses ersten CD-Spielers von Philips, dem CD 100.
Die Entstehung des Oversamplings schilderte er in einem Bericht, hier aus dem Englischen übersetzt:
"Wir bei Philips argumentierten, dass es unmöglich sei, in kurzer Zeit den fertigen 14-Bit-Wandler auf 16 Bit umzukonstruieren.
Aber mein Kollege Karel Dijkmans meinte:
Kein Problem, ich kenne einen kleinen Trick, um unseren 14-Bit-Konverter in einen mit 16 Bit zu verwandeln.
Der Trick heißt Oversampling.
Das Marketing wird dann aus der Not die Tugend machen.
Je stärker die Baudichte in der weiteren Entwicklung der Chips wuchs, je mehr Funktionen implementiert wurden, desto mehr schwanden die Chancen, die einmal eingeschlagene, falsche Richtung korrigieren zu können.
Heute gibt es kaum noch Wandlerchips, die auf eingebautes Oversampling und komplette Ausgangsstufen einfachster Machart verzichten.
Diese Wandler ermöglichen es zwar, Millionen kleiner Handys und MP3-Spieler billigst zu produzieren.
Vom Ideal naturgetreuer Wiedergabe entfernen sie sich zunehmend.
Somit haben sie in einem hochwertigen Musik-Wiedergabegerät nichts zu suchen.
Das Dilemma der Entwickler ist heute, dass sie nicht mehr auf andere Chips zurückgreifen können.
No Oversampling
Durch Entfernung der Digitalfilter wird die zeitliche Präzision der Musikwiedergabe hörbar verbessert.
Der Klanggewinn ist allerdings von einer Reihe ineinander greifenden Modifikationen abhängig.
Der "Vorteil" der eingesetzten Digitalfilter liegt in der Reduzierung nachfolgender Analogfilter - und nicht in einer Datenerhöhung durch Interpolation, um etwas hinzuzufügen, was gar nicht im Signal vorhanden ist.
Das ist in den Datenblättern dieser Digitalfilter ausgewiesen.
Analogfilter, die den Hörbereich über 20 kHz filtern sollen, sind mit zunehmender Flankensteilheit (was eine bessere Filterwirkung bewirkt) in der Produktion teurer.
Sie sorgen auch für nachteilige Phasenverschiebungen im Hörbereich.
Die in den Philips-Spielern verbauten Digital-Decoder (welche vor dem serienmäßigen Digitalfilter sitzen) sind nach offiziellen Angaben der Entwickler für den direkten Betrieb an Analogwandlern ohne Digitalfilter zulässig - auch das wird eindeutig in den Datenblättern beschrieben.
Theoretisch müsste aus Sicht eines Audio-Entwicklers beim Betrieb ohne Digitalfilter der analoge Filter mit einer größeren Flankensteilheit arbeiten.
Wie in den ersten CD-Spielern von Sony praktiziert.
Von den Befürwortern des no-Oversamplings wird häufig argumentiert, dass eine Filterung nicht benötigt wird, da das menschliche Gehör diese Frequenzen nicht wahrnehmen kann. Die Praxis zeigt jedoch, dass auch vermeintlich nichthörbare Frequenzen eine bessere Empfindung der räumlichen Präzision vermitteln.
Mit zunehmender Frequenz nimmt bekanntlich die Schallbündelung zu.
Dadurch ist die Schallquelle mithilfe mehrerer Empfänger besser zu identifizieren.
Obwohl der Mensch nur zwei Empfänger (Ohren) besitzt und der Informationsinhalt selbst nicht bewusst wahrgenommen wird, wird der räumliche Eindruck bei der Reproduktion deutlich gesteigert.
Die Musik wird durchsichtiger, Instrumente oder Stimmen trennen sich klarer voneinander.
Man kann also aus gutem Grund auf Oversampling und Analogfilter verzichten.
Allerdings wird die alleinige Wirkung von No-Oversampling, also der Entfernung der Digitalfilter, leicht überschätzt.
Der Vorteil liegt sozusagen darin, dass die (unvermeidbaren) Nachteile der Digitalfilter eliminiert werden.
Für die Musikwiedergabe bedeutet das: Es werden Artefakte beseitigt, die im Ursprungssignal gar nicht vorhanden sind.
Diese entstehen bei der Überlagerung mehrerer Samples, von denen einige vom Ursprungs-Sample abweichen.
Daneben sorgt der fehlerhaft arbeitende Digitalfilter für eine Verunreinigung der digitalen Spannungsversorgung.
Die 14 Bit Philips-CD-Spieler stellen mit ihrer weitestgehend diskreten Bauart einen unschätzbaren Wert dar. Eine Befreiung von den Digitalfiltern ist in ihnen aber nur ein Schritt von vielen.
Daneben sollte eine umfassende Restaurierung die konstruktive Basis für alle ineinander greifenden Maßnahmen bereiten.
attenuated no oversampling bridge
Datenformat 44.1khz/16bit
Es ist spannend etwas Neues zu erschaffen.
Manche schnappen sich einen Lötkolben, andere starten eine Computer-Simulation.
Jeder scheint sein eigenes Konzept zu besitzen.
In meinem Fall beginnt es mit dem Zurückgehen zu den Grundlagen.
Nach Prüfung der folgenden zwei Aspekte, kam ich zu dem Schluss, dass es problematisch ist, das Ursprungssignal durch Oversampling zu verändern.
1. Oversampling und Jitter
Es gibt zwei Achsen bei der Digitalisierung des Tons.
Die Zeitachse und die Amplituden-Achse.
Im Falle der CD betragen diese 44,1khz und 16 Bit.
16 Bit Genauigkeit bedeutet, wie genau sich die akustische Energie (Zeit x Amplitude), in jedem der 16 Bit-Schritte verteilt.
Mit anderen Worten, wir packen in die Amplitude jedes der 16 Bit alle 22,7µsec. Daten.
Daraus resultiert eine Fehlerrate von maximal +0,5 LSB.
Diese Fehler betreffen aber nur die Amplituden-Achse, auf der Zeitachse sind keinerlei Fehler zugelassen.
Je genauer die Amplituden-Daten sind, desto einfacher lassen sich Fehler auf der Zeitachse verteilen.
Wenn wir die Hälfte (1/2) der Fehler verteilen ergibt sich (1 ÷ 44,1khz ÷ 2 hoch 16) ÷ 2 = 173psec.
Das ist die Obergrenze der zulässigen Fehler, des Jitters.
Bild 1
aktzeptable Fehler bei 44.1khz/16Bit
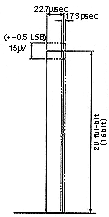
Bild 2
aktzeptable Fehler bei 8x Oversampling/20Bit
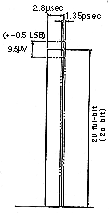
Bei 8x Oversampling und 20 Bit würde diese Fehlerrate 1.35psec. bedeuten.
Das hört sich erstmal gut an, ist aber nicht von einem Analog Wandler zu erreichen, da dieser länger benötigt seine zeitliche Taktung mittels PPL zurück zusetzen.
Daraus folgt, dass bei einem durchschnittlichen Jitter-Umfeld, Oversampling die Genauigkeit innerhalb des Arbeitsumfelds sogar sinken lässt.
Kurz und einfach, durch Oversampling bleiben die ursprünglichen Daten mit 16 Bit Genauigkeit nicht erhalten.
2. Oversampling und High-Bit
Ursprünglich wurde Oversampling entwickelt, um die Verwendung eines analogen Filter mit sanfteren Eigenschaften zu ermöglichen.
Ein weit verbreiteter Irrtum ist dessen Absicht zur Datenerhöhung - auch wenn dieses resultiert.
Bild 3
Das Prinzip der digitalen FIR Filter ist die ursprünglichen Daten zu verschieben und sie zu überlagern.
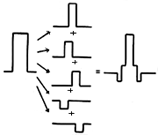
Wenn diese Überlagerung durch Multiplikation der Koeffizienten auf die ursprünglichen Daten gelegt wird, wollen nun viel mehr Daten in das 16 Bit breite Datenfenster.
Diese höhere Datendichte kann nur mit einem breiteren Fenster, also höheren Bit Rate als die 16 Bit der Quell-Daten, transportiert werden.
Zum Beispiel beim digitalen Filter SM5842 beträgt diese Datenfensterbreite 32 Bit.
Der Digitalfilter rundet diese bei der Ausgabe auf 20 Bit ab und erzeugt bei der Re-Quantitisierung weitere Fehler.
Solche Fehler können generell nur mit dem Beibehalten der ursprünglichen Datenfensterbreite von 16 Bit ausgeschlossen werden.
Damit sind wir nicht in der Lage das höhere Datenvolumen, selbst wenn wir dieses beabsichtigt hätten, in der ursprünglichen Datenfensterbreite von 16 Bit zu transportieren.
Ein 16 Bit ohne Oversampling ist immer genauer als ein Oversampling und High-Bit.
Bild 4 - Fortsetzung des Bildrauschens
Was wird ohne Oversampling passieren?
Theoretisch wird das Bildrauschen stufenlos zu höheren Frequenzen (Bild 4) wiederholt werden.
Eine konventionelle Antwort hierauf wäre, das klingt nicht schön.
Und, um das Bildrauschen zu entfernen sollten steilflankige Analogfilter mit anderen Nachteilen dem Analog Wandler folgen.
Ist das so?
Eine Herausforderung wäre nun auf das Shannon-Theorem über die Übertragung von Informationen einzugehen.
Ich halte aber die Wahrnehmung von Informationen für wichtiger.
Die Beschränkung unseres Hörsinns ist ein leistungsfähiger Tiefpass-Filter und das Shannon-Theorem kann sich getrost damit zufrieden geben.
Über Theorien und Oszilloskope kann ich keinen guten Klang hören.
Man kann denken, dass Frequenzen, die Menschen nicht hören, gefiltert werden müssten.
Allerdings können auch 8x Oversampling Filter nur Frequenzen zwischen 22,05 kHz und 330kHz ausschneiden.
Alles über 330kHz bleibt unberührt, es liegt also auch hier Hoffnung auf ein positives Ergebnis zu Grunde.
Ich teile diese Hoffnung, es wird kein Problem sein.
Ein Problem ist nur in den Begleiterscheinungen dieser Filter begründet.
Probleme des Digitalfilters
Bild 5 zeigt das Prinzip der FIR Digitalfilter.
Das "T" steht für eine Verzögerung bei jedem Abtastintervall, "a" ist für den Koeffizientenmultiplizierer und "+" ist der Addierer.
Nach Verzögerung der Eingabedaten und multiplizierung mit dem Koeffizienten wird dieser Prozess "n" mal wiederholt.
Wobei "n" die Anzahl der Wege ist. Je mehr Wege der Filter hat, desto höher soll seine Leistung sein.
Die Verzögerung ist keine Berechnung der Zeit, sondern eher die Wartezeit der Daten.
Bild 5
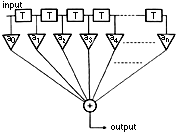
T: Delay Schaltung für jedes Abtastintervall
a: Koeffizientenmultiplizierers
+: Addierer
Bild 6
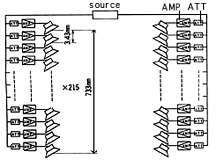
Akustische Wirkung
Es ist gar nicht leicht dieses Diagramm instinktiv zu verstehen.
Der Vorgang wird an Bild 6 etwas deutlicher.
Die Verzögerungs wirkt wie eine Zeitversetzung des Schalls.
Die kumulierte Verzögerung für jeden Weg beträgt 1,92msec, 0,16msec und 0,05 msec. Insgesamt sind es 2,13msec.
Unser Hörsinn kann alle 2msec eine Frequenzanalyse durchführen. Eine Verzögerung von 2,13msec kann unser Ohr wahrnehmen.
Der wahrnehmbare Abstand zwischen dem vorderen und hinteren Lautsprechern entspricht akustisch 73,3cm.
Können sie sich nun vorstellen welche Art von Musik so erzeugt wird?
Alle Töne aus den Lautsprechern werden sich zeitversetzt zu einem kleinen Echo versammeln.
Bild 7 zeigt die sinngemäße Anordnung der Aufnahmemikrofone.
Wenn Sie immer fühlten, dass bei einer digitalen Aufnahme etwas Kern im Ton fehlte, überprüfen Sie bitte diese Darstellung aufmerksam.
So Aufzunehmen und alles zu vermischen macht keinen Sinn.
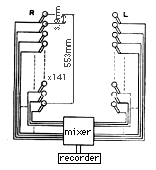
Genau so unsinnig ist aber die Aufnahme mit nur einem Mikrofon bei Verwendung eines digitalen Filters.
Ein digitaler Filter machte auch theoretisch nur Sinn, wenn seine Verzögerung deutlich weniger als die wahrnehmbaren 2msec betrüge.
Ryohei Kusunoki, MJ Magazine (Zusammengefasst u. Übersetzt. AS.)

 Worldwide shipping from Germany - free from 50€
Worldwide shipping from Germany - free from 50€





